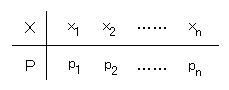確率変数

０から36までの数字を書いたルーレットがある。 ある数字に１ドルを賭け、その数字に入ると36ドルもらえる。 それ以外の数字なら１ドルを損する。 儲けの平均値を求めよう。 これは問題ないとおもいます。 いつものようにまず「払い戻し額」で考えれば 36(1/37)＋0(36/37) ＝　0.973 （ドル） が期待値で、 「儲け」で考えれば、1ドルに対して0.973ドルなので、 0.973-1= -0.027 （ドル） になります。 あるいは、結果が２つしかないので直接求める方が簡単です。 35(1/37)＋(-1)(36/37) ＝ -0.027 （ドル） これが「テラ銭」ですね。 テラ銭＝控除率＝2.7％です。 さてＸは、二種類のリターン、36 or 0 をとる変数です。そしてその変数は確率を伴うので「確率変数」といいます。 また、確率変数を表にしたものを確率分布表といいます。 確率変数、確率分布表 Ｘが有限個の値、 x1, x2, ……, xn をとる変数で、 Ｘ＝x1, x2, ……, xn となる確率が順に p1, p2, ……, pn のように与えられているとする。 ただし p1+p2+ …… +pn = 1, pi≧0 このとき、変数Ｘを確率変数（または変量）といい、 p1, p2, ……, pn を Ｘの確率分布という。またこの値を示す下のような表を確率分布表という。 さらにＭ＝x1p1＋x2p2＋ …… ＋xnpn を確率変数Ｘの平均という。