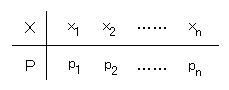分散

つぎのような２つの賭けを考えてみてください。（必ずプラスになる賭けです。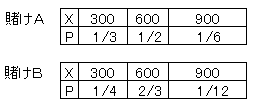） 　 例によってまず期待値を計算します。 賭けＡ： 300(1/3)+600(1/2)+900(1/6)=100+300+150 = 550 （万円） 賭けＢ： 300(1/4)+600(2/3)+900(1/12)=75+400+75 = 550 （万円） 期待値は同じです。 しかし、結果のばらつき方が違います。 そこで、何かばらつきの目安になるものがあれば便利です。 それが「分散」というものです。 分散の定義 確率変数Ｘの分布が、次のように与えられたとする。 このとき、Ｘの平均を m とし、次のような確率変数（Ｘ−m）2 を考える。 この（Ｘ−m）2 の平均のことを、はじめのＸの分散という。 定義にしたがって分散を計算します。 Ｘの平均とは期待値のことで、m＝550 　 V(A) = (-250)2(1/3)+502(1/2)+3502(1/6) = 42500 V(B) = (-250)2(1/4)+502(2/3)+3502(1/12) = 27500 分散は　V(A)＞V(B)　。 そして、もとの確率分布表を見ると、Ｂのほうが中央寄りです。 分散が小さいと確率分布が中央寄りになるのです。 このように分散は確率変数のとる値のばらつきを見る目安を与える数値です。