|
今回は「和の法則」です。
BIGの確率が 1/240 、REGの確率が 1/480 のとき、ボーナスのトータル確率はいくらか
というときに
(1/240)+(1/480) = 1/160 とやります。
これが和の法則です。
ふだんあたりまえに使う和の法則ですが、そもそもこれはなぜ成り立つのでしょう。
和の法則はパチスロの抽選の仕組みから理解できます。
パチスロはレバーを叩いたときに抽選が行われます。
機械内部ではコンピュータが0から16383まで 16384 ( = 214) 個の数字を超高速でカウントしていて(数えていて)、レバーを叩いたときにどの数字をカウントしていたかによって、当選する役が決まります。
ニューパルサー設定6の場合、16384個のうち、各役に当選となる値の個数が次のようになっています。
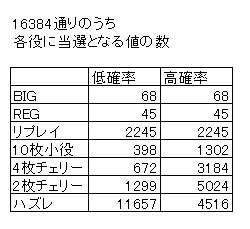
パチスロでは通常、2種類の状態(モード)があります。
小役が当たりやすいのが高確率状態、小役が当たりにくいのが低確率状態です。
ボーナス(BIG/REG)とリプレイの当たり方は同じです。
レバーを叩くことが試行です。そして、
起こりうるすべての場合の集合(16384通り)が全事象、
集合の要素(各役に当選となる値)が根元事象です。
各役に当選する確率というのは、これらの個数をそれぞれ16384で割ればいいわけです。
たとえば、
16384の根元事象のうちBIGとなる根元事象が68通り、だからBIGが当たるという事象の確率は 68/16384 となります。部分集合/全体集合 ということです。
そうして求めた確率が下の表です。
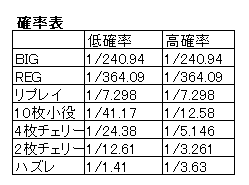
BIGが当たることを事象A、REGが当たることを事象Bとします。
1つの値には1つの役しか対応していないので、
つまり、BIGとREGが同時に当たったりはしないので、
事象Aと事象Bは排反事象です。
このとき、試行結果が16384通りある中で、
Aとなる場合が68通り、Bとなる場合が45通りあるので、
AかBになる場合は(68+45)通り。
よってAかBになる確率は (68+45)/16384 = 113/16384 = 1/144.99
これがBIGかREGが当たる確率、すなわちボーナスのトータル確率です。
|
和の法則
事象をAとBに場合分けするときには、AとBに共通の場合がないことが望ましい。
そのようなとき、A、Bは排反事象であるといわれる。
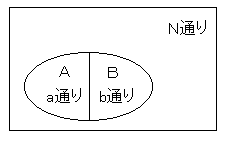 このとき、試行結果がN通りある中で、
Aとなる場合が a 通り、Bとなる場合が b 通りあれば、
AかBになる場合は (a+b) 通り。
AかBかという事象をA∪Bで表すと
このとき、試行結果がN通りある中で、
Aとなる場合が a 通り、Bとなる場合が b 通りあれば、
AかBになる場合は (a+b) 通り。
AかBかという事象をA∪Bで表すと
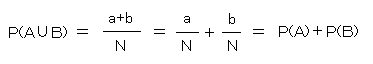 これを和の法則という。
これを和の法則という。
|

|  和の法則
和の法則
 和の法則
和の法則