大数の法則

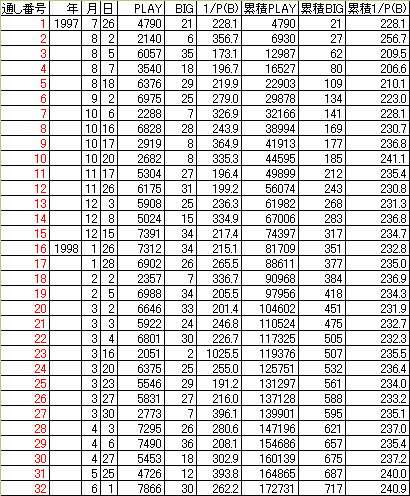
下の表は、1997年7月〜1998年6月の1年間に管理人が打ったニューパルサー設定5の データです。これを見ると、累積確率が設定5のBIG確率 1/240.9 に収束していく様子がわかります。 これが有名な「大数の法則」です。 試行回数を n 、成功回数を r とします。 大数の法則は、この成功率 r/n が、 n が大きくなるに従って、真の確率 p に近づくことを保証するものです。

「大数の法則を確認したいから」。これがデータをとる１つの大きな理由です。 ◆大数の法則 いま、BIGの確率を 1/241 とします。 BIGを○、ハズレを×で表すとします。 いま10プレイ打って次のような結果だったとします。 ｛××○×××××××｝ ○×では扱いにくいので、 1,0 で表すことにしましょう。 つまり、BIGなら1点、ハズレなら0点とするのです。 ｛0, 0, 1, 0, 0, 0, 0, 0, 0, 0｝ こうすればBIG出現率は、平均得点として考えることができます。 すなわち (0+0+1+0+0+0+0+0+0+0)/10 = 1/10 （点） 20プレイ目には次のような結果になっていたとしましょう。 ｛0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0｝ 平均得点は 1/20 （点） 大数の法則は、この平均得点が、プレイ数が増えるにしたがって、 1/241 に近づくと言っているのです。 1/241 とは何でしょうか。 1(1/241) + 0(240/241) = 1/241 つまり1回のプレイの期待値です。 よって、確率収束するとは、1プレイの期待値に近づくということです。 大数の法則　　いま、試行回数を n 、成功回数を r 、真の確率を p とする。 このとき、成功率 r/n は n が大きくなるに従って、真の確率 p に近づく。 言いかえると、成功率 r/n は p に確率収束する。 すなわち、 任意のε＞0 に対して、 N→∞ のとき、P(│r/n - p│＞ε) → 0　 ◇データの抽出方法