自然対数の底

逆数ハマリの確率は e-1 不思議ですよね、これは。 e-1 = 0.367879 例えば大工の源さんで、確率分母＝439回転ハマる確率は y = (1-(1/439))439 = 0.367460 これは自然対数の底 e の逆数とほぼ同じ値です。驚いたことに パチンコでもパチスロでも確率分母だけハマる確率は常に e-1 = 0.367879 なのです。こんなに便利な目安はないです。 同時に、確率分母だけ回せば当たる確率はいつも 1-e-1 = 0.632121 。 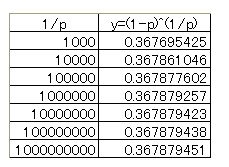p が 0 に近づくほど y は e-1 に近づきます。 かなり大きい p でもそれなりの値になります。 簡単な証明を示しておきます。 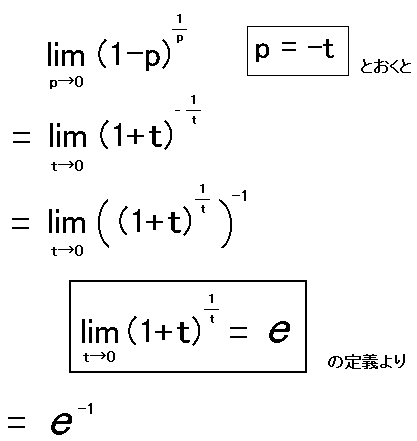★ e e は「ネーピアの常数」ともいい、なんか常に出てくる数なんですね。 e は無理数で、e = 2.718281828… 。鮒一鉢二鉢一鉢二鉢と覚えます。 英語で覚えるなら、 "To express e, remember to memorize a sentence to simplify this." というのがあります。単語の長さに対応させるのです。直訳すると「eを表現するには、eを簡単にするための文を覚えなさい」。おもしろいですね。 とにかくこの 0.6321 という数字は便利です。たとえば いま管理人のMP3のフォルダには24曲入っていて、それをランダムで聴いているんですけど、いま一番お気に入りの曲が、演奏開始後24曲以内にかかる確率は？とか考えるときに、多少の誤差はありますが 0.6321 、と計算するまでもないので便利です。