 情報量
情報量
|
確率というのはいつも1以下なので、確率の計算はいつも分数か小数の計算です。
でも分数や小数をそのまま扱うのはなにかと大変です。
そこで確率を次の式で変換しておくと、場合によっては少し計算がラクになるかもしれません。
I(A)のことを「情報量」と呼ぶことにしましょう。 たとえば、BIG が当たったときの意外性は、チェリーが当たったときの意外性とは比べものにならないぐらい大きいです。なぜ意外性が大きいのかというと、それはむろん確率が低いからです。また、意外性が大きいということは、われわれの得た情報が大きいと考えることができます。そこで、事象の確率が低いほど大きい情報と言えるので、「情報量」という名前は悪くありませんよね。単位ですか? 底が2なので、 binary digit (2進数)を略した bit なんかどうでしょう。 実際にいろんな大当たり確率を情報量に直してみましょう。 2を bit 乗すると確率分母になります。 「万が一」は「13ビット」。なんだかクールですね。 情報量が10をこえると、それは ものすごい価値であるということがわかります。
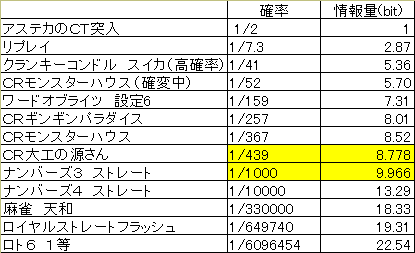 (天和の確率は概算値)
それでは確率の計算がラクになるとはどういうことでしょう。 たとえば「大工の源さんが1回転目で当たる」 「ナンバーズ3を1口だけ買って当たる」 という2つの好運なことを考えましょう。 互いに独立な事象なので、この2つが続けて起こる確率というのは、
I(A∩B)
シャノン(Claude Elwood Shannon)
|
