負の二項分布

今まではハマリを1回のBIGで考えていましたが、 これを数回のBIGで考えてみようというのが 「負の二項分布」です。 たとえばBIG確率 1/241 で、554プレイ以上ハマる確率は10％ ですが、BIG5回を引くために、3560プレイ以上使う確率は0.1％です。 負の二項分布が二項分布と違う点は、 二項分布がBIG回数を変数にするのに対し、 負の二項分布はプレイ数を変数にするということです。 ◆二項分布 確率 p をもつ事象が n 回の観察で x 回起こる確率は P(x) = nCxpxqn-x である (q=1-p) 。この式で表される確率分布を二項分布という。 確率 1/241 のBIGが、1000プレイでちょうど5回当たる確率 は P(1000) = 1000C5(1/241)5(240/241)995 = COMBIN(1000, 5)*(1/241)^5*(240/241)^995 = 0.162 です。 Excel には二項分布のための関数が用意されており、 ふつうは、BINOMDIST関数（false）で求めます。　 書式は　BINOMDIST(成功数, 試行回数, 成功率, 関数形式)　です。 よって BINOMDIST(5,1000,1/241,0) = 0.162 になります。　 ◆負の二項分布 1回の観察においてある事象が起こる確率を p とする。その事象が r 回起こるまでに x 回の観察を行なわなければならないとすれば、 x は r, r+1, r+2,…… の値をとる確率変数であり、その確率分布は P(x) = x-1Cr-1prqx-r である (q=1-p) 。これを負の二項分布という。 ＜証明＞ (x-1) 回目までに(r-1) 回○で、最後 x 回目に○ということだから x-1Cr-1 × ( pr-1q(x-1)-(r-1) × p ) 当たりがたとえば5回くるまでに、いったい何プレイぐらいしなければならないのだろう、 とかいうのを考えるときがこれです。 いま、BIGの確率を 1/241 とします。BIGが5回くるまでに行なうプレイ数は確率変数です。 5回くるまでのプレイ数とは、5回目が何プレイ目にくるかということです。 5プレイ目に5回目がくる確率は (1/241)(1/241)(1/241)(1/241)(1/241) = (1/241)5 6プレイ目に5回目がくる確率。5プレイ目までに4回当たり、 6プレイ目で5回目が当たるということなので、 これはつぎのような5通りのケースが考えられます。 ○○○○×　○ ○○○×○　○ ○○×○○　○ ○×○○○　○ ×○○○○　○ それぞれの確率は (1/241)5(240/241)1　 ですから、 確率は　 5C4(1/241)5(240/241)1　 です。 同様に考えて、7プレイ目に5回目がくる確率は、 6プレイ目までに4回当たり、 7プレイ目で5回目が当たるということですから、 6C4(1/241)4(240/241)2*(1/241) =6C4(1/241)5(240/241)2 です。 結局、 x プレイで5回くる確率は　 P(x) = x-1C4(1/241)5(240/241)x-5 = COMBIN(x-1, 4)*(1/241)^5*(240/241)^(x-5) 負の二項分布にも関数が用意されています。 NEGBINOMDIST 関数というのがそれです。 negative binomial distribution の略です。 書式は NEGBINOMDIST(失敗数, 成功数, 成功率) です。 P(x) = x-1C4(1/241)5(240/241)x-5 = COMBIN(x-1, 4)*(1/241)^5*(240/241)^(x-5) = NEGBINOMDIST(x-5, 5, 1/241) を　 x = 5, 6, ……　で計算します。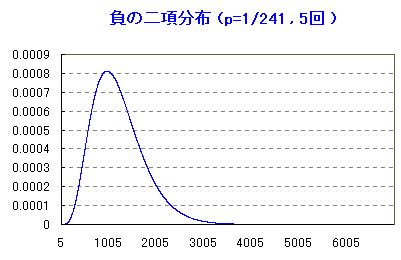 BIG確率 1/241 の場合、5回目のBIGを引く確率が最も高いのは 　 964 または 965 プレイ目で、確率は 0.000812337　です。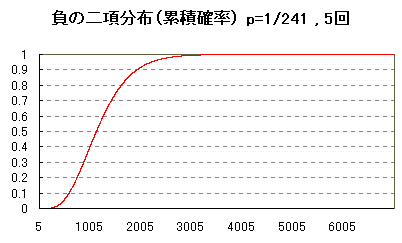 1126プレイ目までに5回目を引ける確率は50％ 1925プレイ目までに5回目を引ける確率は90％ 2204プレイ目までに5回目を引ける確率は95％ 2793プレイ目までに5回目を引ける確率は99％ 3560プレイ目までに5回目を引ける確率は99.9％ このようなことを、いろいろなBIG回数でやってみたのが次の表です。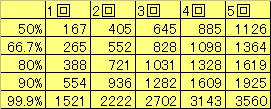 BIG確率 1/241 ※表の見方：　たとえば「2700プレイ打てば99.9％の確率で3回引く」のように見ます。