二項分布２

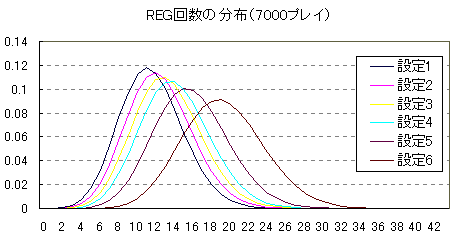
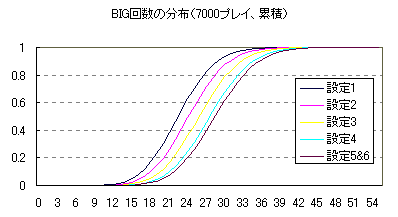
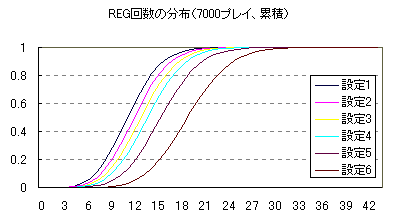
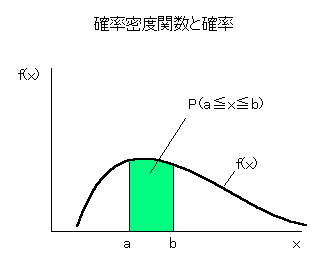
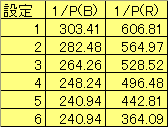
前回の「二項分布」では、二項分布は＜プレイ数が十分に大きければ＞正規分布で近似できるということをお話ししました。でも、 Excel があれば、別に近似しなくても、直接二項分布の確率が求められます。 パチスロの確率論はすなわち二項分布です。 今回は二項分布の確率を Excel を使って求める方法を紹介します。 さて、ジャイアンツの松井選手の背番号55というのは、王貞治選手が1964年に記録したシーズンのホームラン記録で、これを超えるという意味が込められています。 そして、この55という数字は、 BIG確率 1/241 で、7000プレイ打って、BIGがx回以上出る確率というのが99.9999％ ありえない最小のxです。 つまり、（試行回数7000、成功率 1/241 ）の二項分布で、成功回数が 55回以上というのは0.0001％以下の確率です。万が一のレベルをはるかに超えます。 そこで、55回までの確率をプロットしてみたのが次のグラフです。 平均 7000*(1/241)=29 （回）のときが最大値で確率は 0.074 です。 Excel の二項分布のための関数は、BINOMDIST関数というものです。 binomial distribution （二項分布）の略です。 書式は　BINOMDIST(成功数, 試行回数, 成功率, 関数形式)　です。ツールバーの fx をクリックし、BINOMDISTを選びます。 関数形式は TRUE(1) が累積分布関数で、 FALSE(0) が確率密度関数です。 上のグラフは確率密度関数で、BINOMDIST(成功数, 7000, 1/241, FALSE) を、 成功数0〜55について計算したものです。 確率密度関数は、ちょうど＜成功数＞回の成功が得られる確率です。 そして下のグラフが累積分布関数で、 BINOMDIST(成功数, 7000, 1/241, TRUE) を、 成功数0〜55について計算したものです。 累積分布関数は、 多いときで ＜成功数＞回の成功が得られる確率です。 つまり、確率をどんどん足していったものです。 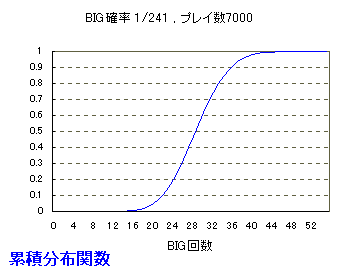これは、 上の確率密度関数のグラフの、下の部分の面積のグラフなのです。 上のグラフで29回を境に確率は小さくなっていくので、下のグラフは29回を境に グラフの伸びが鈍化していくのです。 確率密度関数 f(x) をもつ連続確率変数 x が a と b (a＜b) の間の値をとる確率 P(a≦x≦b) は、 f(x) を区間　[a, b] の間で積分したもの、すなわち で定められる。すなわちそれは、 f(x) の表す曲線の下の部分の区間 [a, b] の面積である。 いろいろな設定で計算し、グラフを描いてみます。 ニューパルサー