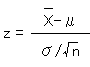中心極限定理
中心極限定理
| いま、二項分布 B(n, 1/241) を考えます。 二項分布のグラフは n が大きくなるにしたがってベル形の曲線に近づきます。 |

|
ベルヌーイ試行に対する中心極限定理は古くから知られています。
平均 np 、分散 npq の正規分布 N(np,npq) に近づくということなので、 上のように標準化された Sn* は標準正規分布に従います。
◆一般の中心極限定理は次のようなものです。 確率変数 Xk の和 ∑Xk の分布、 あるいは平均 ∑Xk/n の分布は正規分布に近づく。
あるいは
これはすごいことです。どんな分布でもその平均は正規分布というのですから、 驚きです。 ◆二項分布の場合は次のように考えます。 いま、BIGの確率を 1/241 とします。 BIGを○、ハズレを×で表すとします。いま10プレイ打って次のような結果だったとします。 {××○×××××××} ○×では扱いにくいので、 1, 0 で表すことにしましょう。つまり、BIGなら1点、ハズレなら0点とするのです。 {0, 0, 1, 0, 0, 0, 0, 0, 0, 0} 合計得点は1点。 ところで、 1, 0 は確率変数です。 よって合計得点は 10個の確率変数の和と考えられます。 合計得点はBIG回数に等しいです。 よって、BIG回数の分布は、 確率変数の和の分布と考えることができます。 そこで中心極限定理は、 Sn = X1 + X2 + … + Xn とすれば、 Sn(BIG回数) あるいは Sn/n (BIG出現率) が正規分布に近づくと言っているのです。 大数の法則が Sn/n → μ と言っているのに対し、 中心極限定理は Sn/n の分布が正規分布に近づくと言っています。
|

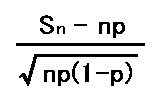
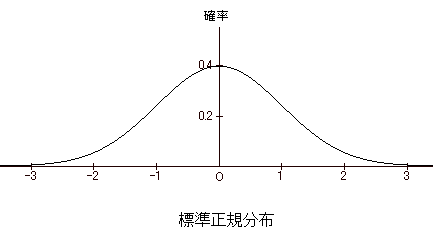
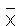 は、標本サイズ n が大きくなるにつれて、平均μ、標準偏差 σ/√n の正規分布に近づく。
は、標本サイズ n が大きくなるにつれて、平均μ、標準偏差 σ/√n の正規分布に近づく。