標準偏差
標準偏差
|
管理人は高校の頃、この標準偏差の「標準」という意味がわかりませんでした。
数学でいう標準とは何なのだ?と思っていました。
高校を出て確率論を勉強してからようやく意味がわかりました。
何のことはありません。みんなが使ってるから「標準」なのです。
統計学にはいろんな「偏差」があって、その中でもよく使われるから「標準偏差」
なのです。標準OSとか標準ブラウザとかと同じです。
標準偏差とは、平均値からの「ずれ」の平均のことです。 言いかえれば平均からのズレの期待値ということです。 分散のルートをとったものが標準偏差ですが、これだけではよくわかりません。 とりあえず、いま知りたいのはパチスロのことなので、 二項分布の標準偏差を考えます。 二項分布の平均は np 、分散は npq です。 高校の頃習ったかと思いますが、その証明が導関数を使ったりして大変だったと思います。 これはもうあきらめて覚えておきます。 逆にいえばそれだけ覚えておく価値があるということです。 したがって二項分布の標準偏差は √npq になります。 打率.250の新庄選手と、打率.350のイチロー選手の400打数の二項分布を考えてみましょう。 平均と標準偏差は次のようになります。  ここで Excel の出番です。2人の BINOMDIST(安打数, 400, 打率, FALSE) を、安打数0〜400について計算してみましょう。  標準偏差の意味はこういうことです。 平均から標準偏差だけずれる確率を求めます。
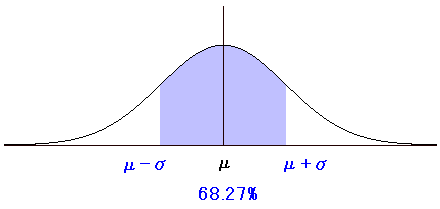
新庄選手が92安打以上108安打する確率は 0.6737 なんか似たような数字ですね。 じつは平均から標準偏差だけずれる確率は 約68.27%なのです。 逆に言うと、確率が、平均を中心として約68.27%の範囲に なるようなラインを決めるのが標準偏差なのです。
μ(ミュー)は平均、σ(シグマ)は標準偏差を表す記号です。 |