正規分布

今回は正規分布の話です。 つぎのような形の曲線を正規分布といいます。 ・ベルをふせた形である ・左右対称である ・平均が中央にある さて、前回の「標準偏差」で見た、新庄選手とイチロー選手のヒット本数の分布です。 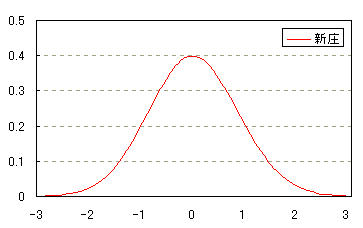安打数 x を z = （安打数−平均）/ 標準偏差 で新しい変数にしましょう。 するとおもしろいことが起きます。 まったく同じグラフになってしまいました。しかも、これはどこかで見たことがあります。 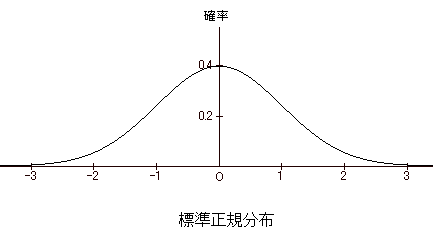なぜこんなことになったのでしょう。 これはまず、「安打数−平均」で、元の分布が平均0の分布に移動します。 そして「安打数−平均」に 1/σ を掛けることで、元の分布のσが 1 になります。たとえば新庄選手なら、100 を引いて 1/8.66 を掛けることにより、 92安打以上108安打というのを -1≦z≦1 に合わせてしまうのです。 平均μ、標準偏差σの正規分布をする変数 x を標準化すると z = (x−μ)/σ になる。 z は、平均0、標準偏差1の正規分布をする。 さて、この標準化はおもしろいばかりではありません。 めちゃくちゃ役に立つのです。標準化すると、 Excel がなくても、 「標準正規分布表」というのさえあれば、たとえば イチロー選手が150安打以上する確率がたちどころに求められるのです。 これを標準化すると z = (150-140)/9.54 = 1.048 で、 z≧1.05 になる確率は 14.69％ と表に書いてあります。 もっと細かく知りたい場合は z = (149.5-140)/9.54 = 0.9958 と補正して、z≧1.00 になる確率15.87％が求められます。 実際の値が15.96％なので、誤差は 0.1％以下です。