 ナッシュ均衡４ |
 |
囚人のジレンマの無限回繰り返しを考えます。
繰り返しゲームで戦略というのは「おうむ返し」「トリガー戦略」のような「行動計画」のことです。繰り返し囚人のジレンマでの戦略は他にどんなものがあるでしょう。最も簡単なのは「つねに裏切り」あるいは「つねに協調」です。
いまたとえばヒトミが「つねに裏切り」をとっているとします。 マキはどうするでしょうか？「つねに協調」というのは明らかに馬鹿げています。 「おうむ返し」「トリガー」はどうでしょうか。これも馬鹿げています。 初回の協調がムダに終わるだけです。 いまマキのとれる戦略は「おうむ返し」「トリガー」「つねに裏切り」「つねに協調」 の4つしかないとしましょう。するとヒトミの「つねに裏切り」に対するマキの最適反応は「つねに裏切り」です。 逆にマキが「つねに裏切り」をとっているとしましょう。 ヒトミのとれる戦略も「おうむ返し」「トリガー」「つねに裏切り」「つねに協調」 の4つしかないとします。するとマキの「つねに裏切り」に対するヒトミの最適反応はやはり「つねに裏切り」になります。 （マキ、ヒトミ）＝（つねに裏切り、つねに裏切り）という戦略の組は「互いに最適反応」になります。つまりナッシュ均衡です。これが繰り返しゲームでのナッシュ均衡の考え方です。
いまマキとヒトミは「おうむ返し」「トリガー」「つねに裏切り」「つねに協調」 の4つの戦略しかとれないとします。 ナッシュ均衡は（つねに裏切り、つねに裏切り）だけでしょうか。 調べてみましょう。まず利得表をつくります。
繰り返しゲームでの利得はすでに見たように割引利得の総和です。 いまマキの将来利得に対する割引因子がδであるとしましょう。 そしてヒトミがトリガー戦略をとっているとします。 このときマキが 「つねに協調」をとるとすると： 利得は 3/(1-δ) 「つねに裏切り」をとるとすると： 利得は 5 + δ/(1-δ) 「トリガー」をとるとすると： 利得は 3/(1-δ) 「おうむ返し」をとるとすると： 利得は 3/(1-δ) となります。（計算がわからないときは「無限繰り返しゲーム」を見てください。） これで利得表の一部ができたことになります（下図）。 |
| |
|  |
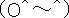
| この調子で残りの枠も埋めていくことができます（下図）。ぜひ確認してみてください。 ヒトミの「つねに協調」に対してマキが「つねに裏切り」をとるとすると、 利得は5の連続なので総割引利得は 5/(1-δ) です。ヒトミの「つねに裏切り」に対して マキが「つねに協調」をとるとすると、利得は0の連続なので総割引利得は 0/(1-δ) です。 「つねに裏切り」をとるとすると、利得は1の連続なので総割引利得は 1/(1-δ) です。 「トリガー」をとるとすると、利得は初回0、あとは1の連続なので総割引利得は 0 + δ/(1-δ) です。ヒトミの「おうむ返し」に対して「つねに裏切り」をとるとすると、利得は初回5、あとは1の連続なので総割引利得は 5 + δ/(1-δ) です。 これで利得表のマキの部分はできました。 |
|
| |
|
|  |
| ヒトミの将来利得に対する割引因子もδであるとします。 ヒトミの部分はこれをy=-xで折り返せばいいので、けっきょく下の利得表が出来上がります。 |
|
| |
|
|  |
| しかしこれではあまりにも見にくいので 1-δ （＞0）を掛けておきます。 数字の大小関係は変わらないので問題ありません。 |
|
| |
|
|  |
|
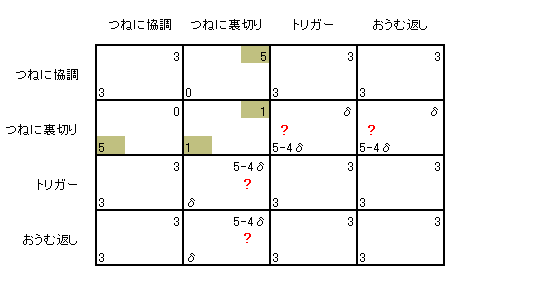
では利得表を調べてみましょう。 0＜δ＜1 に注意します。 まずわかるのは「つねに裏切り」の組はやっぱりナッシュ均衡だということです（下図）。δの大きさに関係ありません。 |
|
| |
|
|  |
|
そして
5-4δ＞3 or δ＜1/2 のとき |
|
| |
|
|  |
|
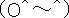
5-4δ＝3 or δ＝1/2 のとき
|
|
| |
|
|  |
|
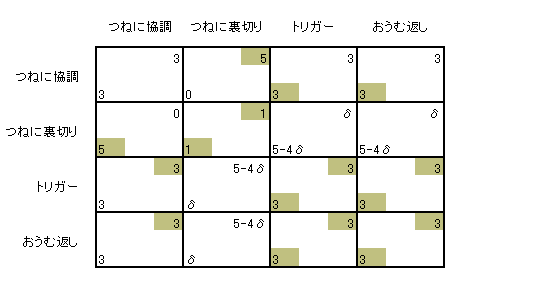
5-4δ＜3 or δ＞1/2 のとき
|
|
| |
|
|  |
|
であることがわかります。
割引因子δが十分に大きいとき（δ≧1/2のとき）、つまり 「マキとヒトミが十分辛抱強いとき」あるいは 「2人の関係について先の見通しが十分に立つとき」 トリガー戦略やおうむ返しによって協調が達成されうるということです。 1回きりの囚人のジレンマではけっして実現しない協調行動が 繰り返しゲームになることで実現します。 この簡単なモデルには強力な含意があります。 つまり第3者（政府など）の強制に頼らなくても プレーヤーたちが処罰を内在した戦略をとることによって 協調が達成されうるということです。
◆参考文献
|
