無限繰り返しゲーム 無限繰り返しゲーム |
 |
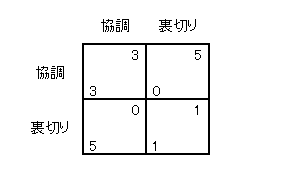
| 今回は囚人のジレンマを無限回繰り返すゲームを考えます。
これは「おうむ返し」で見たマナカナのゲームと同じです。
このゲームでのおうむ返し戦略の有効性はすでに紹介しました。
今回紹介するのはトリガー戦略というものです。 トリガー(trigger)とは銃の引き金のことで、そこから転じて「きっかけ」とか「はずみ」という意味があります。トリガー戦略とは、最初は協調で始めるが、いったん裏切られたらその後永久に裏切り続けるというおそろしい戦略です。
マキとヒトミは毎月このゲームを繰り返すとします。利得の単位を「百万円」として 毎月神様がお小遣いをくれるとしましょう。 いま、ヒトミがトリガー戦略を使うとします。
マキは今月協調すれば300万円もらえます。 来月からも協調すればずっと300万円もらえます。 いっぽう、今月裏切れば500万円もらえます。 しかし来月からはずっと100万円です。 このときマキはどうするべきでしょう。 これは協調したほうがよさそうです。なぜなら、 よい関係を保っておけば 300, 300, 300, 300 ・・・ 今月裏切ってしまうと 500, 100, 100, 100 ・・・ という利得の流れになり、長期的に見れば明らかに協調したほうがトクだからです。 ところがマキが
と考えて将来の利得をずいぶん割り引いて評価するとしましょう。 たとえば、 よい関係を保っておくときの利得の流れを 300, 120, 48, 19.2 ・・・ 今月裏切るときの利得の流れを 500, 40, 16, 6.4 ・・・ と考えるのです。 すると上は初項300、公比0.4の無限等比級数(→「破産する確率」参照)なので和は 300/(1-0.4) = 500 となり、裏切ったときの利得のほうが大きくなります。 すなわちマキが割引因子* 0.4 を用いるときは裏切ることになり、協調は達成されません。 けっきょくいま割引因子をδ(デルタ)とすると、 よい関係を保っておくとき 300 + 300δ + 300δ2 + 300δ3 + ・・・ = 300/(1-δ) 裏切るとき 500 + 100δ + 100δ2 + 100δ3 + ・・・ = 500 + {100δ/(1-δ)} となって、 300/(1-δ) > 500 + {100δ/(1-δ)} のとき協調が達成されることになります。 この不等式を解くと
(1-δ>0を両辺にかけて)
となります。 マキが将来をまあまあ高く評価するときに協調が達成されることになります。
<割引因子> 次回の300を300δ、次々回の300を300δ2・・・といま評価するときこのδを割引因子といいます。またこの評価を将来利得の現在価値といいます。0<δ<1です。割引因子は辛抱強さとかゲームの継続確率とかいろいろに解釈できます。 (→「割引現在価値」も見てください。) ◆参考文献

|