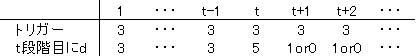ナッシュ均衡５

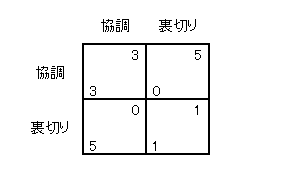
ふたたび囚人のジレンマの無限回繰り返しを考えます。 前回の「ナッシュ均衡４」では戦略を4つに限って考えました。 そこでは「つねに裏切り」の組、とくに割引因子が十分に大きいときは「トリガー」の組、「おうむ返し」の組が ナッシュ均衡となることを見ました。 ところがじつはこれらの戦略の組は 他のすべての可能な戦略を考えても ナッシュ均衡になるのです。 たとえば「つねに裏切り」の組は明らかです。 お互いが「つねに裏切り」をとっているとき 自分だけ一方的に他の別な戦略にかえてみても何にもいいことが ありません。 マキとヒトミがお互いに「つねに裏切り」戦略をとるとします。 マキの利得の流れは 　1 1 1 1 1 1 ... のようになります。ヒトミの「つねに裏切り」を前提とすると マキは「つねに裏切り」から離脱するインセンティブが ありません。どこかで協調cをとるような戦略は利得を低下させるだけです。 今回はとくに「トリガー」の組がナッシュ均衡になることを見てみます。 ヒトミがトリガーをとると仮定しましょう。 もしマキもトリガーをとるとすると 協調行動が発生し、マキの 利得は表の上段のようになります。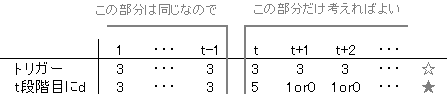 　 いっぽう、マキがトリガーをやめてこれよりも利得を上げよう とすることはけっきょくどこかで協調行動から離脱することを意味します。 じっさいトリガーをやめて結果を変えようとおもえば どこかで裏切らなくてはいけません。 そこでいま考えるべき戦略というのは 第t段階目（t=1, 2, ...）に初めて裏切りdを指定するような戦略です。 このような戦略をとると 利得は表の下段のようになります。 上段と下段を比較します。 第t-1段階目までの割引利得和は同じです。 なので第t段階目以降を考えればいいです。 マキの割引因子をδとします。 (1) トリガーをとるとします。第t段階目以降から得られる利得の現在価値の和☆は A = 3δt-1 + 3δt + 3δt+1 + … = 3δt-1/(1-δ) です。 　 (2) トリガーから離脱するとします。 裏切ったところ（第t段階目）以降から得られる利得の現在価値の和★はせいぜい B = 5δt-1 + 1δt + 1δt+1 + … = 5δt-1 + {δt/(1-δ)} = {5δt-1(1-δ)/(1-δ)} + {δt/(1-δ)} = {(5δt-1-5δt)/(1-δ)} + {δt/(1-δ)} = (5δt-1-4δt)/(1-δ) です。 (3) AとBの大きさを比較します。 A - B = {3δt-1/(1-δ)} - {(5δt-1-4δt)/(1-δ)} = (4δt-2δt-1)/(1-δ) = 2δt-1(2δ-1)/(1-δ) 0＜δ＜1 より δt-1＞0 、また 1-δ＞0 です。 したがって 2δ-1≧0 or δ≧1/2 のとき A≧B となります。 以上の議論よりδ≧1/2のとき★は☆より大きくなれない、 すなわち☆≧★となることがわかります。 これはδ≧1/2のときトリガーから離脱するインセンティブがない ことを意味します。 つまりトリガーは最適反応ということです。 ヒトミについても同様の議論ができます。 δ≧1/2のときトリガーの組はナッシュ均衡です。 　＜　数値例だよ〜 たとえばδ=0.95としてt=13段階目に裏切るとすると ☆は A = 3δt-1 + 3δt + 3δt+1 + … = 3δ12 + 3δ13 + 3δ14 + … = 3δ12/(1-δ) = 3*0.9512/0.05 = 32.4 ★はたかだか B = 5δt-1 + 1δt + 1δt+1 + … = 5δ12 + 1δ13 + 1δ14 + … = 5δ12 + {δ13/(1-δ)} = {5δ12(1-δ)/(1-δ)} + {δ13/(1-δ)} = {(5δ12-5δ13)/(1-δ)} + {δ13/(1-δ)} = (5δ12-4δ13)/(1-δ) = (5*0.9512-4*0.9513)/0.05 =13.0 12段階目までの割引利得和は 初項3、公比0.95の等比数列の第12項までの和（→等比数列の和は「破産する確率」参照）なので S = 3(1-0.9512)/(1-0.95) = 27.6 トリガーをとるとき：　S+A = 27.6+32.4 = 60 離脱したときたかだか：　S+B = 27.6+13.0 = 41 　＜　となっていいことはないんだね〜 tにどんな値をいれても マキの割引因子δが十分大きければ ☆≧★です。 どこに裏切りを指定してもいいことがありません。 ◆参考文献 『ゲーム理論入門』　 　 武藤滋夫、日経文庫、2001年 『ゲーム理論』　 　 岡田章、有斐閣、1996年