男と女 男と女 |
 |
|
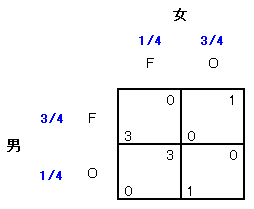
ここにあるカップルがいます。男と女はフットボール (F) に行くかオペラ (O) に行くかを決めなくてはいけません。男は女といっしょにいたいとおもっていて、またそのときはどちらかというとフットボールのほうがよいです。
ところが問題は、男は女の選好についてよくわからないことです。 とくに男は、女が自分といっしょにいたい (Loving) のか、それともひとりで行動したい (Leaving) のか、よくわかりません。 いま、男と女は、下のいずれかのゲームをやっているとします。
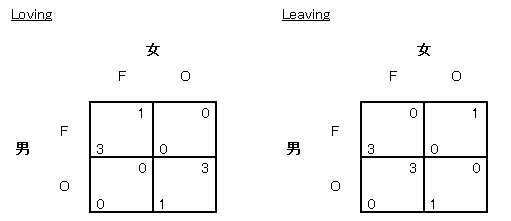
女はじっさい、どっちのゲームをやっているかわかっているのですが、男はそれがわかりません。男は左のゲームに確率ρ、右のゲームに確率 1-ρ を割り当てます。(ρは「ロー」と読みます。) このゲームは、新しいプレーヤー Nature を導入して、つぎのように変換できます。
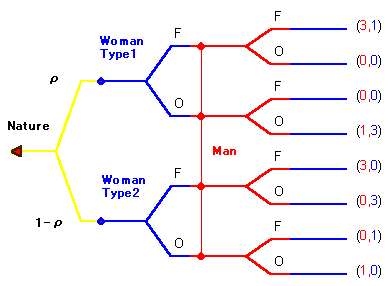
( Loving をタイプ1、 Leaving をタイプ2とします。女は自然の選択を知ることができて、男はこれができないと考えます。) さて、男の純粋戦略は F か O の選択です。混合戦略は F を選ぶ確率です。いまこの確率をλとします。(λは「ラムダ」と読みます。) いっぽう、女の純粋戦略は、 <タイプ1での選択> と <タイプ2での選択> の組合せで、 (F, F), (F, O), (O, F), (O, O) の4通りです。そして混合戦略は (μ1, μ2) の組合せになります。ここで、 μ1 はタイプ1で F をプレイする確率、 μ2 はタイプ2で F をプレイする確率です。(μは「ミュー」と読みます。) そこで、このゲームにおけるベイズ・ナッシュ均衡は、つぎのような (λ, μ1, μ2) の組になります。すなわち、
(1) μ1, μ2 はそれぞれ最適反応
◆ベイズ・ナッシュ均衡(純粋戦略)
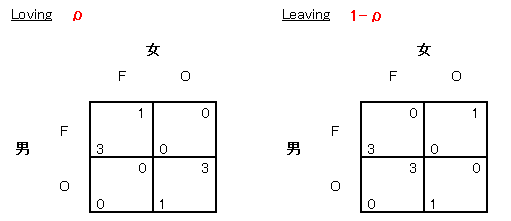
まず、 ρ ≧ 1/4 ならば、 (λ, μ1, μ2) = (1, 1, 0) はベイズ・ナッシュ均衡であることがわかります。 いま、男が必ず F をプレイする、すなわち λ = 1 としましょう。すると女は、タイプ1では F 、タイプ2では O をプレイする(μ1 = 1, μ2 = 0 )のが最適反応です。 逆に、女の (F, O) を前提とすると、男は F をプレイすることによって期待利得 3ρ + 0(1-ρ) = 3ρ を得ます。 O をプレイすることによって期待利得 0ρ + 1(1-ρ) = 1-ρ を得ます。 したがって、 3ρ ≧ 1-ρ 、すなわち ρ ≧ 1/4 ならば F は男の最適反応になります。 こうして、 タイプ1である見込みが少なくとも 25% あれば、男が F をプレイし、女が (F, O) をプレイすることは、ベイズ・ナッシュ均衡であることがわかります。

ベイズ・ナッシュ均衡はもう1つあります。 ρ ≧ 3/4 ならば、 (λ, μ1, μ2) = (0, 0, 1) はベイズ・ナッシュ均衡になります。 いま、男が必ず O をプレイする、すなわち λ = 0 としましょう。すると、女はタイプ1では O 、タイプ2では F をプレイする(μ1 = 0, μ2 = 1 )のが最適反応です。 逆に、女の (O, F) を前提とすると、男は F をプレイすることによって期待利得 0ρ + 3(1-ρ) = 3-3ρ を得ます。 O をプレイすることによって期待利得 1ρ + 0(1-ρ) = ρ を得ます。したがって、 ρ ≧ 3-3ρ 、すなわち ρ ≧ 3/4 ならば O は男の最適反応になります。 こうしてタイプ1である見込みが少なくとも 75% あれば、男が O をプレイし、女が (O, F) をプレイすることは、ベイズ・ナッシュ均衡であることがわかります。 以上を整理すると、つぎのようになります。
ρ ≧ 3/4 のとき
1/4 ≦ ρ < 3/4 のとき
ρ < 1/4 のとき
◆ベイズ・ナッシュ均衡(混合戦略) 混合戦略まで考えて、つぎのような (λ, μ1, μ2) の組を求めてみます。
(1) μ1, μ2 はそれぞれ最適反応

まず、とっかかりとして、簡単なケースを考えてみましょう。 たとえば ρ = 0 とします。男は女がタイプ2であると100%確信しているということです。これは右のテーブルを考えていることになります。するとこのゲームでは純粋戦略によるナッシュ均衡はありません。しかし混合戦略によるナッシュ均衡はあります。計算は省略しますが、これは (λ, μ2) = (3/4, 1/4) です。(→「ナッシュ均衡2」の問題と同じです。)
ρ = 0 のとき、 (λ, μ2) = (3/4, 1/4) はベイズ・ナッシュ均衡になります。 ▼ いま、ρの値にかかわらず、 (λ, μ1, μ2) = (3/4, 1/4, 1/4) はベイズ・ナッシュ均衡になることを確認してみましょう。 まず、男が確率 3/4 で F をプレイするとします。これを前提にしたときの女の最適反応を考えます。 すると、タイプ1では、 F をプレイすることによって得られる利得は 1(3/4) + 0(1/4) = 3/4 です。そして、 O をプレイすることによって得られる利得は 0(3/4) + 3(1/4) = 3/4 です。 F と O は無差別になります。期待利得が同じものをどうこうミックスしたところで何も変わらないので、とくに μ1 = 1/4 は最適反応になります。

タイプ2では、 F をプレイすることによって得られる利得は 0(3/4) + 3(1/4) = 3/4 です。そして、 O をプレイすることによって得られる利得は 1(3/4) + 0(1/4) = 3/4 です。 F と O は無差別になります。したがってとくに μ2 = 1/4 は最適反応になります。 逆に、女の (μ1, μ2) = (1/4, 1/4) を前提としたときの、男の最適反応について考えましょう。 まず、男が F をプレイするとします。 すると
左のテーブルでの利得は 3(1/4) + 0(3/4) = 3/4
になります。 そして左のテーブルになる確率はρ 、右のテーブルになる確率は 1-ρ なので、期待利得は、
(3/4)ρ + (3/4)(1-ρ)
になります。

いっぽう、男が O をプレイするとします。すると
左のテーブルでの利得は 0(1/4) + 1(3/4) = 3/4
になります。よって期待利得は
(3/4)ρ + (3/4)(1-ρ)
になります。 F と O は無差別になり、したがってとくに λ = 3/4 は最適反応となります。 以上、ρの値にかかわらず、 (λ, μ1, μ2) = (3/4, 1/4, 1/4) はベイズ・ナッシュ均衡になることがわかります。
◆参考文献

|