オランダ式オークション
|
オランダ式オークションとは、オークショニアが
高い価格から始めて徐々に価格を下げていき、
最初に価格を了承した参加者が落札する形のオークションです。
オランダ式オークションの最も簡単なモデルは次のようなものになります。
リカとマリがお宝チケットを争っています。 リカはこのチケットに5万4000円まで払っていいと考えていて、 マリは3万4000円まで払っていいと考えています。 そしてお互いにこのことを知っています。
 VS 
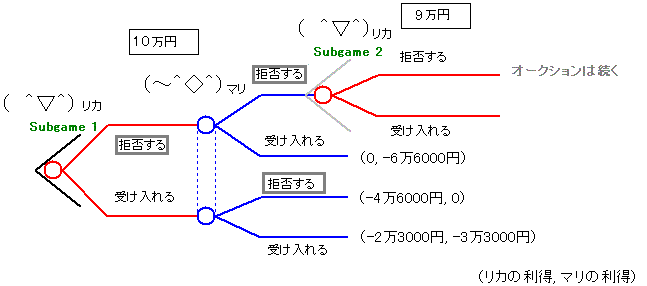
オークションは次のように行われます。 つまりオークショニアが10万円から1万円ずつ価格を下げていき、 オークショニアが価格をコールするたびに、リカとマリは 「受け入れるか、拒否するか」を（同時に）決めます。 どちらかが受け入れたとき、オークションは終了し、 その価格でチケットは落札されます。 2人が同時に受け入れた場合はコイントスで落札者を決めます。 これは有限・動学ゲームであり、 ゲームの最初の部分は下のようなツリーで表されます。 （支払い意思額−価格＝余剰が利得になります。点線で結んだものは情報集合です。） |
|
このゲームで戦略というのは、
「それぞれの価格で受け入れるか拒否するかを定めた計画」のことです。
たとえば戦略の一つは、受け入れるを○、拒否するを×で書くとすると、
（10万円, 9万円, 8万円, . . . , 2万円, 1万円）＝（×, ×, ○, . . . , ○, ○） といったものになります。
このゲームはバックワードインダクションで解けます。 最終ラウンド（subgame10）から考えましょう。 価格1万円ではリカもマリも受け入れるのが絶対優位の戦略になります。
|
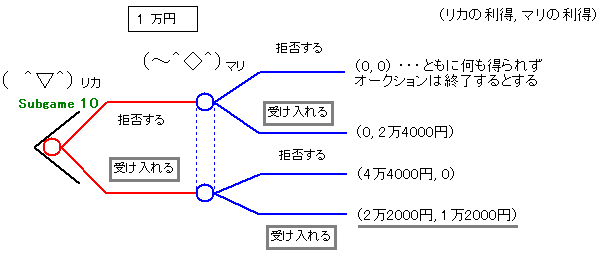
| subgame9。 価格2万円ではリカもマリも受け入れるのが絶対優位の戦略になります。 |
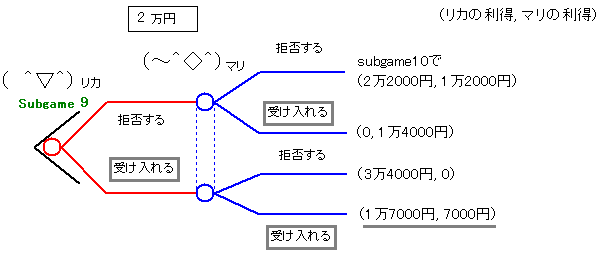
| subgame8。 価格3万円ではリカは受け入れるのが絶対優位の戦略になります。 マリはこれを前提として受け入れる戦略をとります。 |
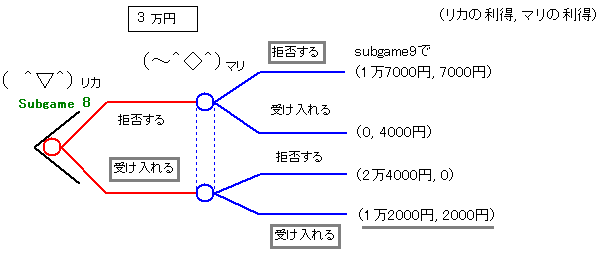
| subgame7。 価格4万円ではリカは受け入れるのが絶対優位の戦略になりますが、 マリは拒否するのが絶対優位の戦略になります。 |
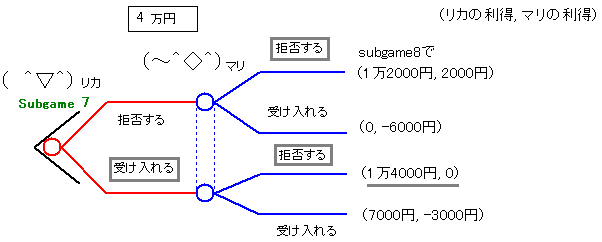
| subgame6。 価格5万円ではマリは拒否するのが絶対優位の戦略になります。 リカはこれを前提として拒否する戦略をとります。 |
|
subgame5以前では価格が6万円なので、落札したとしても利得がマイナスになります。
よって2人とも（常に利得0を確保できる）拒否する戦略をとります。
▼以上より （10万円, 9万円, 8万円, 7万円, 6万円, 5万円, 4万円, 3万円, 2万円, 1万円） ＝（×, ×, ×, ×, ×, ×, ○, ○, ○, ○） がリカの唯一正しい戦略で、 （10万円, 9万円, 8万円, 7万円, 6万円, 5万円, 4万円, 3万円, 2万円, 1万円） ＝（×, ×, ×, ×, ×, ×, ×, ○, ○, ○） がマリの唯一正しい戦略であることがわかります。 ゲームはリカが4万円で落札し終了します。
◆参考文献
|
