|
【定理3】
いま BIG 終了後(カウンタ値は0)のクレジットを A とする。
そして、投入枚数のうち、 割合 r だけをクレジットから入れるとする。
すると、クレジットが A になっているとき、小役払出率 k は r に等しい。
すなわち、CR = A のとき、CR投入率 r が小役払出率 k になる。
<証明>
投入枚数を M とする。
いま、クレジットから rM だけ投入する。
クレジットがAになるとは、rM だけ払出があったということ。
小役払出率 k は k = rM/M = r
|
いま、ハナビを考えます。
BIG終了後にクレジットを30にしておき、
CR投入率が 0.3789 < r ≦ 0.3906 になるように打ちます。
クレジットが30になっているとき、払出率 k はCR投入率に等しく、 0.3789 < k ≦ 0.3906 です。
ハナビの設定5以上の判別プレイは、 0.3789 < k ≦ 0.3906 のときでした。

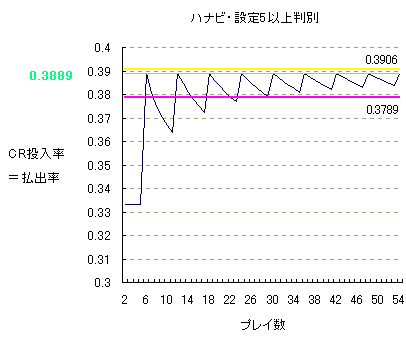
24プレイ目以降では、CR投入率は必ず 0.3789 < r ≦ 0.3906 です。
すなわち、
24プレイ目以降でクレジットが30のとき、
必ず払出率は 0.3789 < k ≦ 0.3906 です。
よって24プレイ目以降でCRが30になるプレイは
必ず判別プレイなのです。
|
【定理4】
CR投入率が、Xプレイ目以降では必ず
ks-1 < r ≦ ks になるとする。
このようなXを判別の解といい、X*で表す。
X*プレイ目以降でCRが A になるプレイは、必ず判別プレイである。
なぜならば、このようなプレイで、CR投入率 r は
ks-1 < r ≦ ks 、
小役払出率 k は
ks-1 < k ≦ ks
だからである。
|
|
 5. 判別法
5. 判別法


