シミュレーション２

今回はランダムウォークの話です。 前回のシミュレーション１で、7000個の INT(RAND()+(1/241)) （0か1）に出玉を対応させれば、玉の出方がシミュレートできます。ただし、話をわかりやすくするために、REG割を小役割に含めておきます。 （ペイアウト率については → 「期待値」） ▼ニューパルサーの設定6を考えます。 BIG純増が373.55枚、REG割が0.33813、小役割が1.42567。 よってまずREG割＋小役割＝1.7638。 したがって、BIGが当たらなかったプレイ（0のプレイ）に対する期待値は、 1.7638-3=-1.2362 よって次のような確率分布表になります。 1/241　で　373.55（枚） 240/241　で　-1.2362（枚） ▼ペイアウト率は　 (1/241)*373.55+(240/241)*(-1.2362)=0.318929461 　 に3を加えて3で割ったもの　 3.318929461/3=1.10630982 です。 よって7000プレイ＝21000枚の投入に対し、 平均して23233枚の払出があり、2233枚の純増です。 ▼次のようにして純増枚数を対応させます。 いまA列は0か1です。B列は1からA列を引いたものとします。 そして C=A*(373.55)+B*(-1.2362) こうすれば A列が0のとき、B列（1-A）は1で純増枚数は -1.2362 A列が1のとき、B列（1-A）は0で純増枚数は 373.55 になります。 そしてC列の和が純増枚数の和になります。 D列にはC列の累積和を作っておきます。 D列をグラフにすればランダムウォークの様子がわかります。 [BIG回数32、純増3340枚]

▼6個の擬似データを作ってみました。いちばん右下のグラフはすごいです。ある人が4万以上突っ込んで帰った後、誰かが一気に7万出しています。 右上も極端ですね。カチ盛りのドル箱が一気に飲まれていく様子を表しています。

[30回,2590枚]　　 　　[22回,-408枚]

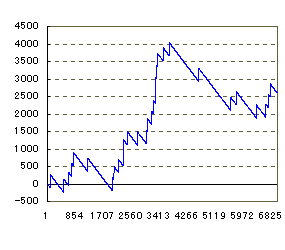
[34回,4089枚]　　 　　[25回,716枚]

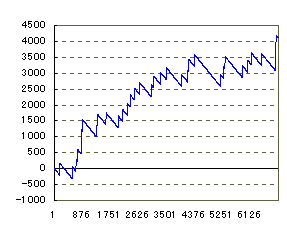
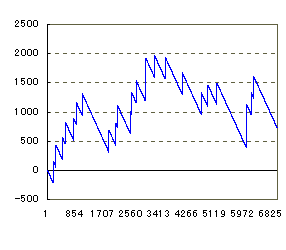
[38回,5588枚]　　 　　[27回,1466枚]

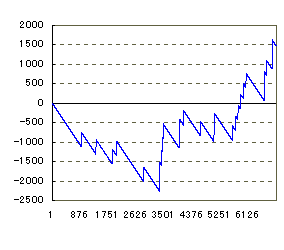
等価交換では(純増枚数/5)*100がそのまま収支になります。 6戦5勝で、最高が11万1000円勝ち、最低が9000円負けとなります。 平均大当たり回数29.3回、平均純増枚数2340枚で、ほぼ理論値通りです。 ▼ ランダムウォークは 直線 y=1.1063x からの「ゆらぎ」であると考えてもよいですし、 あるいは、 ランダムウォークは直線（平均値）へ回帰すると 考えてもよいです。

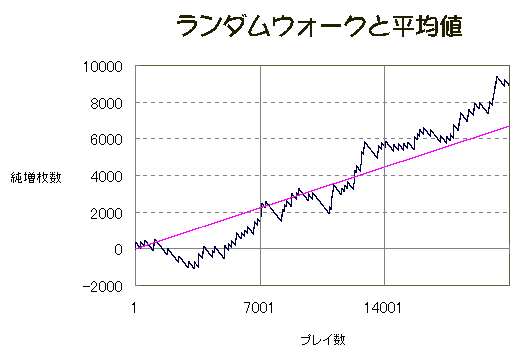
ミクロで見たときのゆらぎが「ツキ」とよばれるものです。 これがあるから長いこと飽きずに打てるのです。