 ナッシュ均衡6 ナッシュ均衡6 |
 |
|
囚人のジレンマの有限回繰り返しはツリーで考えることができました。 そしてバックワードインダクションによりゲームの解を求めることができました。 では無限回繰り返しではどうでしょう。 今回は無限繰り返しの囚人のジレンマで (トリガー、トリガー)の組が部分ゲーム完全均衡になることを説明します。 まず準備のために以下の2点の内容を確認してみてください。 1. チェスはゲームツリーで完全に記述できます。 そしてツリーのどの点にいるかさえわかれば それまでのプレイの履歴がわかります。 あるいは履歴を見ながらツリーを最初からたどっていくと どの点にいるかわかります。
 展開形ゲームで戦略というのは すべての点での行動をもれなく指定したものです。 代理人に渡せる完全なプランのことです。 繰り返しゲームも同じ考え方です。
2. そして
ということです。 これは有限回のときを思い出してもらえれば わかると思います。 3回繰り返しゲームでは第3段階から始まる部分ゲームの数は16でした。 各段階での可能な結果はいつも4通りあります。 2段階が終わったときの可能な結果(履歴)は4*4=16通りです。
以上で準備は終わりました。 さて、 すべての部分ゲームに均衡を導くナッシュ均衡が部分ゲーム完全均衡です。 ナッシュ均衡のうちすべての部分ゲームで合理的になっている ものを部分ゲーム完全均衡といいます。 (この言い方をするのは初めてなので「ナッシュ均衡3」とか「2回繰り返しゲーム」で確認してみてください。)
部分ゲームとはそこだけ切り取って分析できるゲームなので そのゲームでの戦略あるいはナッシュ均衡というのを考えられます。 これまでは部分ゲーム完全均衡をバックワードインダクションという方法で求めていました。それぞれの部分ゲームでの均衡をいちばんうしろから求めていくと 部分ゲーム完全均衡が求まるのでした。 しかし無限繰り返しゲームではツリーが無限のかなたへ伸びていくので いちばんうしろというのはありません。 なので囚人のジレンマの無限回繰り返しでは バックワードインダクションは使えません。 でも部分ゲーム完全均衡を考えることはできます。 囚人のジレンマの無限回繰り返しの部分ゲームは無限にあり、 そしてそれらは囚人のジレンマの無限回繰り返しです。 どこを切り取っても囚人のジレンマの無限回繰り返しです。 どの部分ゲームも全体のゲームと等しいのです。
マキとヒトミのゲームです。 δ≧1/2のときの ナッシュ均衡の1つである(トリガー、トリガー)を考えてみます。 この戦略の組が部分ゲーム完全均衡になっていることはつぎのようにしてわかります。 いま4段階目からの部分ゲームについて考えてみましょう。 3段階目までの可能な履歴は全部で4*4*4=64通りあります。 そしてこのうちの1通りだけが 裏切りを含まないものです。 それ以外の63通りはすべて裏切りが含まれています。(下図。)
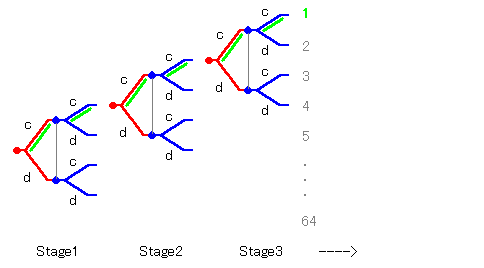
すると4段階目から始まる64個の部分ゲームというのは
それまでの履歴に裏切りを含まないもの (1) と
の2種類に分けられることがわかります。 ところがいま
(1のような)それまでの履歴に裏切りを含まない部分ゲームを タイプA
と呼ぶことにしましょう。 すると、これら4段階目からの部分ゲームだけでなく、他のすべての 部分ゲームがタイプAかタイプBに分けられることになるとおもいます。 5段階目からの256個の部分ゲームは1個のタイプAと255個のタイプBです。 そこでトリガー戦略というのは
タイプAの部分ゲームにはトリガー戦略を
誘導する戦略です。(下図。)
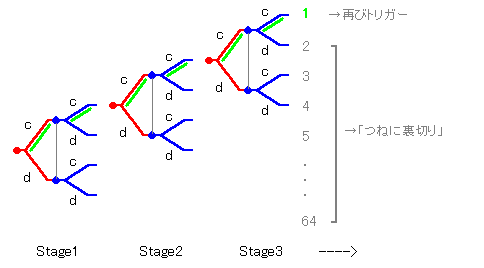
ここがミソなので少し立ち止まって考えてみてください。 元のトリガー戦略は1のような部分ゲームで 再びトリガー戦略をとることを要求します。 (部分ゲームとはそこだけ切り取って分析できるゲームなので そのゲームでの戦略というのを考えられます。) つまり再び「裏切りが発生するまで協調する」戦略を この部分ゲームでとることを要求します。 また元のトリガー戦略は2-64のような部分ゲームに 「つねに裏切り」戦略を誘導します。 問題はこれらの部分ゲームでこれらの誘導された戦略が均衡を形成するかどうかということです。 答えはYESです。なぜなら まず 1. どの部分ゲームも全体のゲームに等しいので、とくにタイプAの部分ゲームは全体のゲームに等しいです。 これらタイプAの部分ゲームを分析することは全体のゲームを分析することと同じです。 (どの部分ゲームも改めて第1段階目からのゲームと考えます。) 全体のゲームでトリガー戦略の組はナッシュ均衡でした。 ということはこれらタイプAの部分ゲームでトリガー戦略の組はナッシュ均衡ということです。 そして 2. どの部分ゲームも全体のゲームに等しいので、とくにタイプBの部分ゲームは全体のゲームに等しいです。これらタイプBの部分ゲームを分析することは全体のゲームを分析することと同じです。(どの部分ゲームも改めて第1段階目からのゲームと考えます。) 全体のゲームで「つねに裏切り」戦略の組はナッシュ均衡でした。 ということはこれらタイプBの部分ゲームで「つねに裏切り」戦略の組はナッシュ均衡ということです。

こうして元のトリガー戦略の組は
タイプAの部分ゲームにトリガー戦略の均衡を 導くことがわかります。 これは元のトリガー戦略の組が部分ゲーム完全均衡となっていることを 意味します。
でもいったいこれで何がわかったんでしょうか。 部分ゲーム完全均衡というのははったりを見抜くための概念です。 (→「ナッシュ均衡3」参照。) トリガーの組が部分ゲーム完全均衡になっているということはすなわち ヒトミが「裏切ったらこわいよー」と言ったとき、 マキが「よっすぃーはお人よっすぃーだからこっちが裏切っても本当にキレることはないだろう」と考えることはできない ということです。 トリガーという処罰戦略は確かに抑止力をもつのです。
◆参考文献

|

