ナッシュ均衡と不動点
ナッシュ均衡と不動点
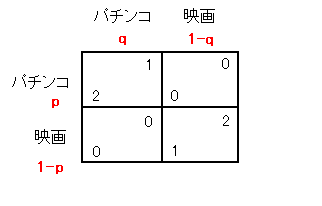
下のアイとノノのゲームは混合戦略まで考えると3つのナッシュ均衡があります。
(わからない方はあいとのぞみ、ナッシュ均衡2、ナッシュ均衡(混合戦略)などを見てください。)
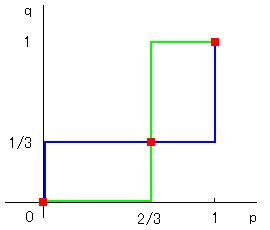
つまり (p, q) = (0, 0), (2/3, 1/3), (1, 1) がナッシュ均衡です。 (青がアイの最適反応、緑がノノの最適反応を表します。) さて、いまある戦略の組 (p, q) をインプットすると、 p, q のそれぞれについて最適反応を調べて、 やはり戦略の組としてある (p, q) を返すという関数Fを考えましょう。 たとえばこの関数は (p, q) = (1/3, 2/3) に対しては (p, q) = (1, 0) を返します。 (上のグラフを見ると、p=1/3 に対してはノノの q=0 が最適反応、 q=2/3 に対してはアイの p=1 が最適反応です。) さてこの関数Fは、たとえば (p, q) = (1, 1) に対しては (p, q) = (1, 1) を返します。 入れたものと同じものを返してくるのですね。数学ではこのような点――初めに入れた (1, 1) ――は不動点 fixed point と言われます。 このアイとノノのゲームについて言えば、他に (p, q) = (0, 0) も不動点です。 しかし (p, q) = (1/3, 2/3) は不動点ではありません。(同じものを返してくるか、こないかについて調べてみてください。) ここで感づかれた方もいるでしょう。 どうやらナッシュ均衡というのは数学的には不動点と一致するらしいと。 そうなのです。じっさい、関数Fが、ある戦略の組 (p*, q*) について調べて、 その結果、 p* に対する最適反応が q* で、同時に q* に対する最適反応が p* であったなら、 関数Fは (p*, q*) を返すでしょう。(元の戦略の組と同じ。) ところがこの (p*, q*) は、その性質上、ナッシュ均衡なのです。 (互いに最適反応。)
◆ナッシュ均衡の存在と不動点定理 つまりナッシュ均衡はある関数の不動点なのです。 したがってナッシュ均衡の存在について考えることは、 ある関数で不動点の存在について考えることと同じなのです。 ある関数が不動点をもつかどうかということは、 数学では詳しく調べられていて、 その内容は不動点定理として知られます。 経済学で最も使われる不動点定理は Kakutani で、 これは一般均衡(完全競争均衡)の存在証明にも、 ナッシュ均衡の存在証明にも使われるという、とんでもない大定理です。 不動点定理を理解するには相当の周辺知識がいるのですが、 効率のいい範囲で次回以降詳しく紹介したいと思います。
◆ある戦略の組 (p, q) に対して関数Fが集合を返す場合
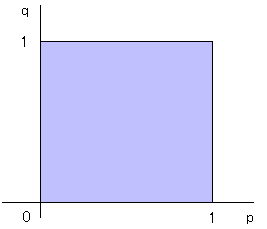
(p, q) = (2/3, 1/3) はナッシュ均衡です。(青:アイ、緑:ノノ) p=2/3に対するノノの最適反応は [0, 1] です。 これは0以上1以下の実数の集合です。 q=1/3に対するアイの最適反応も [0, 1] です。 よって関数Fは (p, q) = (2/3, 1/3) に対しては (p, q) = ([0, 1], [0, 1]) を返すということになります。 しかしこういう場合も元の点を不動点というのです。 これは (p, q) = ([0, 1], [0, 1]) が正方形の中の任意の点を表すからです(下図)。 元の点が、返ってきた集合の中に含まれる場合、それも不動点というのです。
他に関数Fは (p, q) = (2/3, 2/3) に対しては (p, q) = (1, [0, 1]) を返します。 しかし元の点は返ってきた集合の中にないので、不動点ではありません(下図)。
1つの要素に対し多くの要素を返す関数は multi-valued と言われますが、 その multi-value の中に元の要素が入っていればそれは不動点というのです。
◆不動点の定義 (p, q) = (0, 0), (1, 1) のときのように、点に対して点が返ってくるときも、 それは1つの要素しかもたない集合と考えることができるので、 一般に不動点とは x* ∈ F(x*) となる x* のことを言います。(定義) ここで F(x*) は、元の点 x* に対してFが返した集合で、 記号∈は x* が F(x*) の要素であることを意味します。 上の例でいえば
x* = (0, 0) ∈ (0, 0) 不動点はその定義が単純なゆえにおもしろい性質をたくさんもち、またその定理群は応用範囲が広く強力なのです。
以上を要約すると、ある戦略の組に対しては最適反応の組み合わせが作れて、 その関数の不動点がナッシュ均衡だということです。 よってナッシュ均衡の存在は不動点の問題に帰着され、 「ある条件のもとでは関数は必ず不動点をもつ」という不動点定理が使えるのです。 (この「ある条件」については次回以降をお楽しみに。)
◆参考文献

|